이번에 포스팅할 논문은 "Distilling a Neural Network Into a Soft Decision Tree" 로, Nicholas Frosst와 Geoffrey Hinton교수가 쓴 논문입니다. 논문 제목에서 유추할수 있듯이 Neural Network를 Decision Tree와 접목시킨 내용의 논문입니다. 이 모형의 성능 자체는 매우 좋은 것은 아닙니다만, 아이디어가 독특해서 포스팅하게 되었습니다.
Motivation/Introduction
논문에서는 다음과 같이 쓰여져 있는데, 결국에 하고자 하는 이야기는 Neural Net이 좋긴 한데 classification decision 에 대해서는 조금 설명하기 어려운 부분이 있으니 Neural Net을 통해 지식을 취하고 계층적 의사결정을 표현하면 좋겠다!
- Deep neural networks have proved to be a very effective way to perform classification tasks
- But it is hard to explain why a learned network makes a particular classification decision on a particular test case
- If we could take the knowledge acquired by the neural net and express the same knowledge in a model that relies on hierarchical decisions instead, explaining a particular decision would be much easier

Input과 hidden 사이, 그리고 hidden과 output 사이의 unit들은 어느정도 그 역할(원인 또는 영향)을 이해하는 것이 가능하지만(논문에는 이렇게 서술 되어 있지만, 사실상 이것도 힘들..), hidden사이에서의 unit들은 이해하기가 매우 어렵습니다. 반면에 Decision Tree는 누구나 다 알고 있듯이, 계층적으로 classification의 decision을 이해할 수 있기 때문에 해석력에 있어서는 매우 뛰어나다는 장점을 지닙니다.
본 논문에서는 다음과 같이 서술 하며, Decision tree의 해석력과 Neural Net의 powerful 한 성능을 어느정도 절충할 수 있는 모델을 제안합니다. 논문에서는 mimic(모방하다)라는 단어를 써서 Neural Net의 input-output function을 사용한다라고 서술되어 있는데 이는 Neural Net의 layer에서 layer로 넘어갈때 사용하는 식(Wx+b)을 의미하는 것입니다. 본 논문에서 제안하는 모델은 실험결과 Neural Net보다는 좋은 성능을 보이지는 않았으나, 준수한 성능을 보였으며 학습속도와 해석력에 있어서 좋은 결과를 보였다고 합니다. 모델을 지칭하는 단어는 Soft Decision Tree(SDT)입니다.
- we propose a novel way of resolving the tension between generalization and interpretability.
- we use the deep neural network to train a decision tree that mimics the input-output function discovered by the neural network but works in a completely different way.
- 모델의 성능과 해석력을 둘다 높일 수 있는 방법을 제안!
- Decision tree를 학습시키기 위해 Neural Net의 학습형태(WX + b)를 사용.
The Hierarchical Mixture of Bigots
모델을 설명하는 chapter의 제목은 위에 적혀있는 것처럼 "Bigot의 계층적인 혼합"이고 쓰여있습니다. Bigot의 사전적인 의미는 "편견이 아주 심한 사람"인데요. 저도 논문을 읽고 나서도 대체 왜 이런 단어를 사용했는지 이해가 가지 않았지만, 여러번 읽고 나서야 조금이나마 이해가 되었습니다.(논문이 친절하게 모든걸 알려주지는 않습니다 ㅠㅠ). SDT는 Pi의 inner node와 Q의 leaf node로 이루어져 있고 각각에 대한 수식은 아래와 같습니다.(처음에 논문을 읽으면서 매우 간단하다라고 생각했었는데, 자세히 파고들려고하니 그렇게 간단하지는 않더군요)

여기서 주목해야할 부분은 Pi의 수식인데요. i는 inner node의 index입니다. 논문에서는 depth가 2인 Tree를 예로 들어서 (inner node가 한개 뿐이라 잘 이해가 되지 않을 수 있습니다) depth가 3인 Tree를 예로 드는게 좋을 것 같습니다. 아래 그림을 보시면 첫번째, 두번째, 세번째 inner node의 식을 보시면 각각 다른 Weight와 bias를 가지지만 input은 x vector로 같은것을 확인할 수 있습니다. 일반적인 Neural net을 생각해봤을때, input-> hidden1 으로 가고 hidden1 -> hidden2로 갈때 이전 layer에서 나온 값들만을 가지고 계산을 합니다만, SDT에서는 각 inner node는 x vector와 각기 다른 weight를 통해서 만들어 집니다. 즉 하위 inner node의 value는 이전 node value에 의존하지는 않습니다.
각 inner node가 하는 일은 다음 inner node의 왼쪽으로 갈것인지 오른쪽으로 갈것인지에 대한 확률 만을 내보냅니다. 다시 말해, classification은 맨 하위단인 leaf node에서만 수행 됩니다. 예시가 적절한지는 모르겠습니다만 남자,여자,노인,소인에 관한 어떤 데이터가 있다고 가정해보십니다. 이 데이터들에대해 어떤 특정 classification 문제를 푼다고 했을때, 남자는 남자에 대해 집중적으로 잘 분류하는 모델로 예측하고 싶고, 여자는 여자에 대해 집중적으로 잘 분류하는 모델로 예측하고 싶을때 각 inner node가 하는 일은 input data가 들어왔을 때 이 데이터는 남자 데이터에 대해 잘 분류하는 모델을 사용하는게 좋겠다 라고 판단하여 남자 모델이 있는 leaf로 인도하게끔 하는 것입니다. 즉, 여러 leaf node의 다른 모델들을 사용하고, 데이터에 따라 사용하는 leaf node model을 선택하도록 하는 것입니다. 각 inner node들이 예측이라는 것보다는 어떤 모델을 선택할지 도와주고 그때의 weigh들은 이전의 node에 의존하지 않는 독립적인 형태이기 때문에 back propagation 할때에도 이전 node에서 weigth가 전파 되어 오지 않습니다. 즉 inner node는 오로지 그 부분에서 왼쪽/오른쪽 subtree만 분류하는데 집중합니다. 이런 의미에서 Bigots이라는 단어를 사용한게 아닐까 싶습니다.(이 단락에 대한 모든 내용은 논문에 서술 되어 있지 않습니다. 틀렸거나 이상한 부분이 있다면 댓글 달아주세요)
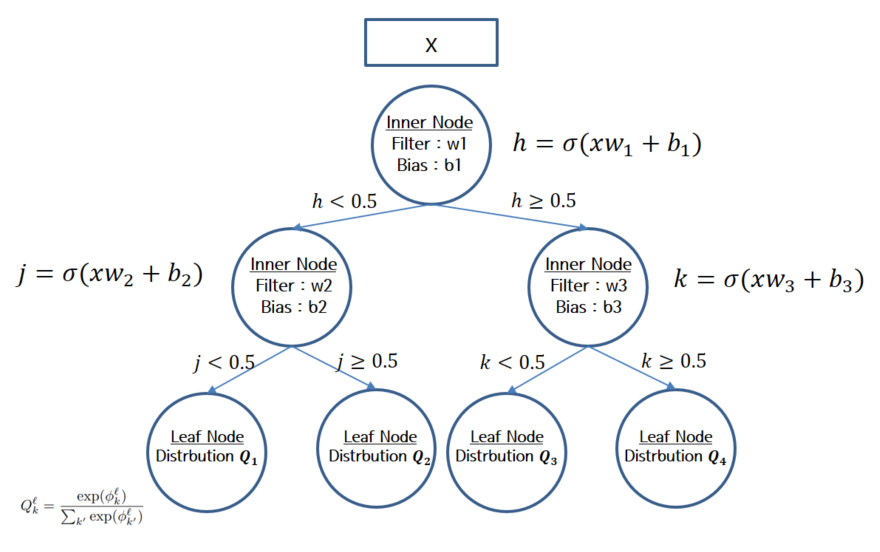
더불어, 이 모델은 Predictive distribution으로 사용될 수 있다고 하는데 사용 방법은 아래와 같습니다. (두가지 방법)
1) 가장 높은 경로 확률을 가지는 leaf로부터의 분포를 사용
- 예측에 대한 설명은 모든 경로에 대하여 필터 목록이 됨
2) 모든 leaf에 대한 분포를 평균내서 사용(각 leaf에 대하여 경로 확률로 가중치를 주어서)
- 예측 성능이 더 높아지나, model의 predictive distribution의 설명 복잡도가 기하급수적으로 증가함
(모든 노드에 대하여 filter를 involve 시키기 때문)
1)에 대한 내용은 모델을 일반적인 Decision Tree처럼 예측시키겠다는 이야기입니다. 위 그림에서 Q1을 선택할 경로 확률은 (1-h)*(1-j)이고 Q4를 선택할 경로 확률은 h * k 입니다. 어떤 데이터가 들어왔을 때 leaf node가 가지는 경로확률이 max인 Leaf node의 모델을 선택해서 분류하고 그 분류에 대한 설명은 path를 거쳐왔던 각 inner node의 filter가 된다는 이야기입니다.
2)에 대한 내용은 모델을 ensemble처럼 사용하여 예측시키겠다는 이야기입니다. 앞서 언급드린 것 처럼 각 leaf node는 경로 확률을 지니고 input이 들어왔을때 각각의 leaf node 모델이 예측하는 prediction output이 있습니다. 이 output에 대하여 각 path 경로 확률로 weight를 주어 최종 prediction output을 내는 것입니다. 예상할 수 있겠지만, 당연히 이 경우에 성능이 더 좋습니다만, 설명 복잡도가 기하급수적으로 증가하게 됩니다.
Loss function은 아래와 같고 Entropy와 비슷한 형태를 지니게 됩니다. 모든 leaf node에서의 error에 대하여 각각의 경로 확률을 곱하여 entropy를 만든 형태 인 것 같습니다.

Regularizers
SDT에서는 Internal node가 left/right sub-tree를 균일하게 사용하게 만들기 위해 penalty term을 추가하는데 만약 Penalty term이 없다면, tree가 안정 상태에 빠지는 경향이 생겨 하나이상의 internal node가 거의 항상 한쪽의 subtree에만 probability를 부여하려 한다고 합니다. 즉 데이터에 따라 다양한 모델을(다양한 leaf node model)을 사용하게 하고 싶은데, penalty term이 없다면 하나의 모델(하나의 leaf node model)만 사용할 가능성이 높다라는 것입니다.
위에서 언급한 Loss 에 아래 Penalty sum을 추가하여 최종적인 Loss를 사용하게 됩니다.
는 노드에서의 평균적인 실제 분포라고 쓰여져 있는데 이부분 이 잘 이해가 되지 않는다면 stochastic gradient를 사용한다고 가정하고 이해하시면 편합니다. X가 하나씩 들어온다면,
로, i번째 노드에서 x를 right sub tree로 분류할 확률이 됩니다.
C는
에 대한 Cross entropy 형태를 띄고 있는데, 기존의 cross entropy는 Y가 1이 되기를 원한다면 여기서는
가 0.5가 되기를 원합니다. 즉, i번째 노드에서 x를 rigth sub tree로 분류할 확률이 0.5가 되기를 바라는 것이죠. Loss를 최소화 시키는 것이기 목적이기 때문에,
가 0.5일때 Penalty도 최소가 될 것이고 이는 아래 그림에서도 확인하실수 있습니다. 왼쪽이 일반적인 Cross entropy, 오른쪽이 SDT의 Penalty 에 대한 그래프 입니다.
inner node 의 확률값에 따라 Penalty sum이 어떻게 바뀌는지 계산하고 싶으시다면 아래 예제를 참고하시면 좋을 것 같습니다.
위 그림에서 j와 k만 변화를 주어서 다시 Penalty 값을 계산하면 아래와 같이 나옵니다. 즉, 상대적으로 inner node의 확률이 0.5에 더 가깝게 (균일하게 node를 분리) 된다면 Penalty sum이 더 낮아지게 됩니다.
Result
SDT를 MNIST Data에 적용한 결과 정확도는 94.45% 가 나왔다고 합니다. CNN (2 conv layer) 의 경우에 99.21 % 정도 나온다는 것을 생각해 보았을 때, 성능 자체는 높은 편인 아니라는 생각이 듭니다. 논문에서는 True label과 Neural Net의 예측을 합성한 Label을 사용하면 정확도를 96.7%까지 높일수 있다고 서술되어 있는데, 여기서 말하는 Neural Net은 SDT를 의미하는것 같고, SDT가 예측한 것을 True 라벨이라 가정하고 재 학습하는 것 같습니다. 논문에서는 성능이 높지는 않지만 Decision Tree처럼 어떤 형태의 filter가 데이터를 어떻게 분류하는지 이해가 가능하다고 서술 되어 있습니다. 아래 그림을 보시면 leaf node와 상위 inner node에서는 잘 구분이 안되지만, 하위노드로 갈수록 특정숫자를 혼합한 모습이 보이기도 합니다. 마지막 leaf node는 softmax로 사용하여 가장 하얀 부분이 Prediction label을 의미하는 것 같습니다. 예를들어 첫번째 leaf node에서 하얀색/검은색 스펙트럼 처럼 보이는곳의 네번째부분이 하얀것을 알수 있고 두번째 leaf node에서는 여섯번째 부분이 하얗게 활성화 되어있는 것을 보실 수 있습니다.
Conclusion
SDT는 Neural Net 보다 좋은 성능은 아니지만, 준수한 성능을 보이면서 Tree와 같은 형태로 activation unit의 역할을 visualization 시킬 수 있다는 장점이 있습니다. (제 생각) 하지만, 이미지 data의 경우에는 filter를 계층적으로 visualization 시키는 것은 의미가 있을 수 있음. 이미지 데이터가 아닌 경우에는 큰 의미가 있을까하는 생각이 듭니다. Kaggle 등 데이터분석 대회에서 대부분 1위를 차지하는 알고리즘인 Gradient Boosting 계열 알고리즘(Light GBM, Xgboost)은 성능도 좋고 중요 변수도 추출 가능합니다. (물론 Tree처럼 시각화 시키는 것은 별개의 일입니다만). 하지만, 성능과는 별개로 모델을 만드는 구조나 학습방식이 매우 독특하기 때문에, 공부할 가치는 있는 모델인 것 같습니다. 현재의 모델을 다른 분야에 접목시키기에는 무리가 있습니다만, 현재 상황에서 좀더 성능을 높일 수 있다면 다양하게 활용될 것 이라 생각합니다.
[PyTorch] 쉽고 빠르게 배우는 딥러닝(할인쿠폰코드) 369-7c698142f82e
https://www.inflearn.com/course/PyTorch-%EB%94%A5%EB%9F%AC%EB%8B%9D
'딥러닝' 카테고리의 다른 글
| [GAN 논문 리뷰] DeLiGAN : Generative Adversarial Networks for Diverse and Limited Data (0) | 2018.06.02 |
|---|---|
| [딥러닝 논문 리뷰] Entity Embeddings of Categorical Variables (0) | 2018.04.08 |
| 알고리즘의 발전 - Drop-out (0) | 2017.04.03 |
| 알고리즘의 발전 - ReLU (1) | 2017.03.25 |
| 딥러닝이란 (0) | 2017.03.21 |









댓글