이번에 소개해드릴 논문은 NEVER GIVE UP: LEARNING DIRECTED EXPLORATION STRATEGIES 이라는 논문으로 2020 ICLR 에 accept된 논문입니다. https://arxiv.org/pdf/2002.06038.pdf
메인 아이디어는 Exploration 과 Exploitation을 같은 네트워크에서 배우게 하는 것이며 이를 위해 Universal Value Function Approximators (UVFA) 를 사용합니다.
논문의 저자들은 다음 두가지 Intrinsic reward 를 제안 합니다.
- Per-episode novelty (Episodic Novelty) : Agent가 여러 에피소드에 걸쳐서 친숙한(familiar) state를 지속적으로 재방문 하도록 함. (같은 에피소드 내에서는 재방문 하지 않음)
- Life-long novelty : 여러 에피소드에 걸쳐 친숙해지는 state들을 점차 하향 조정함 (덜 방문 하도록). RND를 이용하여 계산
본 논문의 main contribution은 다음과 같습니다.
- Life-long novelty 와 Episodic novelty를 결합하여, agent가 지속적으로 exploration을 할 수 있도록 함
- Hard exploration task에서 SOTA (2019년 기준)
논문의 저자들이 언급하는 Intrinsic reward가 가져야할 조건은 다음과 같습니다.
- 한 episode 내에서, 같은 state를 빠르게 재 방문 하지 않도록 함
- 여러 episode에 걸쳐서 많이 방문한 state에 대해서 천천히 방문 빈도를 감소 시킴
- Agent의 action에 영향을 밪치 않은 environment의 state는 무시 (Environment의 배경 등 noise를 무시하려는 것으로 생각됨)
저자들이 제안하는 NEVER GIVE UP (NGU) 의 구조는 아래 그림과 같습니다. Life-long novelty와 Episodic novelty가 결합 된 것을 볼수가 있는데 하나하나 설명드리도록 하겠습니다.

Episodic novelty
Episode가 시작될때 Episodic memory (M) 은 비우고 시작합니다. 모든 스텝에서, agent는 episodic intrinsic reward를 계산하고 current observation 에 해당하는 controllable state를 memory M에 추가합니다. 여기서 episodic intrinsic reward는 agent가 single episode내에서 다양한 state를 방문 하도록 합니다. Controllable state는 environment의 background 등과 같은 (noise) 것에 영향을 받지 않는 feature state를 의미하는 것 같습니다.
State를 embedding network (위 그림의 왼쪽 그림) 에 넣고 controllable state를 추출하고 이를 M에 추가합니다. Embedding network는 state를 controllable 할 수 있도록 representation 하는 과정 인 듯 합니다.
State,와 next state를 Embedding network를 통해 feature state를 추출하고 추출한 feature state를 MLP(one hidden layer)에 넣어 action을 예측합니다. 여기서 action을 잘 예측하면 예측할 수록 Embedding network과 background에 robust한 (noise 등) feature를 추출 할 수 있게 되겠죠(Controllable state). 이는 기존의 curiosity에 관한 컨셉과 동일 합니다 (Curiosity-driven Exploration by Self-supervised Prediction). Embedding network의 전체적인 구조는 아래 그림과 같습니다.

Episodic reward는 다음과 같이 계산 됩니다.
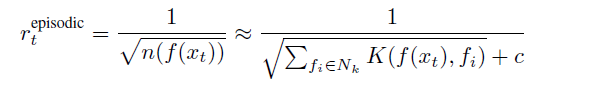
n(f(x))는 state feature를 방문한 횟수를 의미합니다. 물론, discrete 한 feature가 아니기 때문에 단순한 count가 불가능하므로, Kernel function을 이용하여 count와 유사하게 approximate합니다. N_k는 f(x)에 대하여 KNN을 적용하여 구한 neighbor들, 즉 현재 state와 유사한 state를 의미하며 Kernel function은 아래와 같습니다.

d는 euclidean distance, dm은 distance 평균을 의미합니다. K는 일종의 normalized distance라고 볼 수 있겟죠. Embedding된 f(x)와 그 feature의 neighbors인 N_k에 대하여 kernel value를 구하고 이를 KNN의 (k) 번째 neighbor까지 반복 하여 합계를 구하고 역수를 취해서 episodic reward를 구하게 되는 것입니다.
Embedding된 f(x)와 그 feature의 neighbors의 거리가 멀면 멀수록 K값은 작아지고, episodic reward는 이를 역수 취한 것이니 커지게 됩니다. 즉 현재 state의 feature가 주변의 state feature가 멀다면, 현재 feature는 매우 novelty한 특성을 가지고 있다라는 뜻이겠죠. 그러므로 episodic reward를 크게 받도록 하는 것입니다.
Life-long novelty는 RND를 통하여 구하고 (reward Alpha) 다음 식을 통해서 최종적인 Intrinsic reward를 계산합니다. L은 hyper parameter로 본 논문에서는 5로 고정하였습니다.
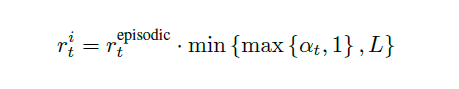
강화학습 구조는 기본적으로 Recurrent Replay Distributed DQN (R2D2)를 사용하였으며, NGU의 intrinsic reward를 vanish되지 않는다 라고 주장하고 있습니다. (최종적인 intrinsic reward는 episodic과 lifelong의 곱셈으로 이루어져 있는데, lifelong음 감소 될수 밖에 없어서 episodic에 따라 달려 있는데 episodic reward는 매 episode마다 M을 초기화 시키기 때문에 감소되지 않아서 그런가 싶습니다..(제 개인적인 생각))
최종적인 reward는 extrinsic reward와 결합하여 다음과 같이 계산됩니다.

이 reward에 관하여 최적의 value function 을 approximate하기 위하 UVFA를 사용합니다 (Q(x, a, b)). Q(x, a, 0) 이면 exploration을 하지 않는 것입니다. 이 부분은 중요한 부분은 아닌 것 같아 넘어가도록 하겠습니다.
성능은 전체적으로 이때 당시를 기준으로 SOTA를 기록 했다고 합니다.
논문의 컨셉을 다시한번 이야기해보면, 기본적으로 RND를 활용하고 prediction error도 함께 사용하였습니다. 여기서 controllable state의 주변 state와 비교하여 novelty 특성을 파악하는 것이 핵심 같습니다. 다만, controllable state를 잘 만들어야 좋은 reward가 발생할 수 있겠네요.






댓글