아래 여러 직선에서 가장 좋은 직선은 데이터의 가운데를 지나가는 직선이라고 할 수 있습니다. 이를 다시 표현하면, 직선을 그었을때 추정치와 실제값의 차이가 가장 작아지는 직선을 의미합니다.

실제 값에서 추정 값을 뺀값을 우리는 잔차 (Residual)이라고 하고, 아래와 같이 ei 또는 ri로 표현하는데 i는 observation number입니다. 즉 i번째 데이터의 잔차를 의미하는 것이죠. 결국에, 이 잔차가 최소가 되도록 직선을 긋는것이 목표가 됩니다.
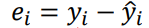
정확히 이야기하면, 우리는 아래와 같이 잔차의 제곱합(Sum of squares error, SSE)이 최소가 되는 직선의 방정식을 구합니다.

그 이유는, 사실 잔차의 합이 0이 되는 해는 무수히 많기 때문입니다. 아래 그림을 보시면 세직선에 대한 잔차를 생각해보면 + 와 - 의 잔차들이 있을텐데, 이는 서로 상쇄되어 모두 0의 값을 가질 수 있습니다.
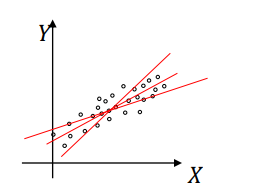
수학적으로 이야기하면, 아래의 잔차의 합이 0 이 되는 해는 무수히 많다라고 이야기 할 수 있습니다.

굳이, 자차의 제곱합이 최소화가 되는 지점을 찾고 싶은 이유는, 잔차의 제곱합의 형태는 다음과 같이 2차 함수 꼴입니다. 가운데가 오목한 형태이기 때문에, 이 함수의 기울기를 구해 0이 되는 지점을 찾으면 잔차의 제곱합이 최소가 되는 지점을 찾을 수 있기 때문입니다. 이 SSE는 결국에, B0와 B1인 회귀계수에 의해 결정되기 때문에, 회귀 계수에 의한 함수라고 바라 볼 수 있으며, 그래서 아래 그림과 같이 X축이 회귀계수로 이루어진 함수로 표현 할 수 있습니다. 즉, 이 SSE는 미분을 활용하여 최소가 되는 지점을 찾을 수 있으며, 그 때의 해는 유일하며 그 해가 회귀계수의 추정치로 사용이 됩니다.

이와 반대로 잔차의 절대값의 합의 형태는 그림으로 표현하면 뾰족한 형태로서 미분이 불가합니다. 그래서 해를 찾기가 어렵습니다. 이러한 이유로, 선형 회귀 모델에서는 SSE를 최소화 하는 방법으로 회귀 계수 B's를 추정합니다.


아래 그림과 같이 SSE를 각각 B0와 B1으로 편미분 하여 연립 방정식을 통해 해를 구할 수 있습니다.

증명 과정은 다음과 같습니다. 보지 않고 증명을 할 수 있는 수준은 아니여도, 한번씩 손으로 풀어보면서 이해를 해보시면 도움이 됩니다.

'데이터사이언스' 카테고리의 다른 글
| 선형 회귀의 결정 계수 (R2) (1) | 2022.12.14 |
|---|---|
| 회귀 계수의 의미 (해석 방법) (0) | 2022.12.14 |
| 선형 회귀 분석 이란 (Linear regression) (0) | 2022.12.14 |
| 부동산 데이터 분석 - '집값이 싼데는 다 이유가 있다'. (1) | 2022.12.11 |
| 인공지능 생성 모델 DALLE 사용하기 (0) | 2022.12.09 |




댓글